Newest Post
// On :Jumat, 28 November 2014
Vectors and Direction
Examples of vector quantities that have been previously discussed include displacement, velocity, acceleration, and force.
Each of these quantities are unique in that a full description of the
quantity demands that both a magnitude and a direction are listed. For
example, suppose your teacher tells you "A bag of gold is located
outside the classroom. To find it, displace yourself 20 meters." This
statement may provide yourself enough information to pique your
interest; yet, there is not enough information included in the statement
to find the bag of gold. The displacement required to find the bag of
gold has not been fully described. On the other hand, suppose your
teacher tells you "A bag of gold is located outside the classroom. To
find it, displace yourself from the center of the classroom door 20
meters in a direction 30 degrees to the west of north." This statement
now provides a complete description of the displacement vector - it
lists both magnitude (20 meters) and direction (30 degrees to the west
of north) relative to a reference or starting position (the center of
the classroom door). Vector quantities are not fully described unless
both magnitude and direction are listed.
Representing Vectors
Vector quantities are often represented by scaled vector diagrams.
Vector diagrams depict a vector by use of an arrow drawn to scale in a
specific direction. Vector diagrams were introduced and used in earlier
units to depict the forces acting upon an object. Such diagrams are
commonly called as free-body diagrams.
An example of a scaled vector diagram is shown in the diagram at the
right. The vector diagram depicts a displacement vector. Observe that
there are several characteristics of this diagram that make it an
appropriately drawn vector diagram.- a scale is clearly listed
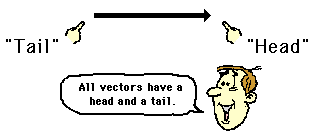
- a vector arrow (with arrowhead) is drawn in a specified direction. The vector arrow has a head and a tail.
- the magnitude and direction of the vector is clearly labeled. In this case, the diagram shows the magnitude is 20 m and the direction is (30 degrees West of North).
Conventions for Describing Directions of Vectors
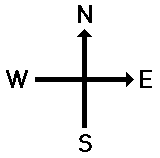Vectors can be directed due East, due West, due South, and due North. But some vectors are directed northeast (at a 45 degree angle); and some vectors are even directed northeast,
yet more north than east. Thus, there is a clear need for some form of a
convention for identifying the direction of a vector that is not
due East, due West, due South, or due North. There are a variety of
conventions for describing the direction of any vector. The two
conventions that will be discussed and used in this unit are described
below:- The direction of a vector is often expressed as an angle of rotation of the vector about its "tail" from east, west, north, or south. For example, a vector can be said to have a direction of 40 degrees North of West (meaning a vector pointing West has been rotated 40 degrees towards the northerly direction) of 65 degrees East of South (meaning a vector pointing South has been rotated 65 degrees towards the easterly direction).
-
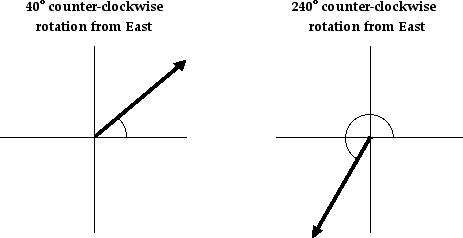
The direction of a vector is often expressed as a counterclockwise angle of rotation of the vector about its "tail"
from due East. Using this convention, a vector with a direction of 30
degrees is a vector that has been rotated 30 degrees in a
counterclockwise direction relative to due east. A vector with a
direction of 160 degrees is a vector that has been rotated 160 degrees
in a counterclockwise direction relative to due east. A vector with a
direction of 270 degrees is a vector that has been rotated 270 degrees
in a counterclockwise direction relative to due east. This is one of the
most common conventions for the direction of a vector and will be
utilized throughout this unit.
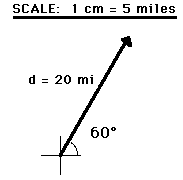Representing the Magnitude of a Vector
The magnitude of a vector in a scaled vector diagram is depicted by the
length of the arrow. The arrow is drawn a precise length in accordance
with a chosen scale. For example, the diagram at the right shows a
vector with a magnitude of 20 miles. Since the scale used for
constructing the diagram is 1 cm = 5 miles, the vector arrow is drawn with a length of 4 cm. That is, 4 cm x (5 miles/1 cm) = 20 miles.Using the same scale (1 cm = 5 miles), a displacement vector that is 15 miles will be represented by a vector arrow that is 3 cm in length. Similarly, a 25-mile displacement vector is represented by a 5-cm long vector arrow. And finally, an 18-mile displacement vector is represented by a 3.6-cm long arrow. See the examples shown below.
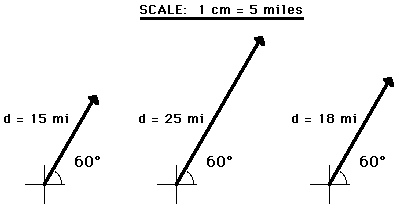
In conclusion, vectors can be represented by use of a scaled vector diagram. On such a diagram, a vector arrow is drawn to represent the vector. The arrow has an obvious tail and arrowhead. The magnitude of a vector is represented by the length of the arrow. A scale is indicated (such as, 1 cm = 5 miles) and the arrow is drawn the proper length according to the chosen scale. The arrow points in the precise direction. Directions are described by the use of some convention. The most common convention is that the direction of a vector is the counterclockwise angle of rotation which that vector makes with respect to due East.
In the remainder of this lesson, in the entire unit, and in future units, scaled vector diagrams and the above convention for the direction of a vector will be frequently used to describe motion and solve problems concerning motion. For this reason, it is critical that you have a comfortable understanding of the means of representing and describing vector quantities. Some practice problems are available on site at the following web page:
Visit the Vector Direction Practice Page
